서론
이진 탐색(Binary Search) 은 정렬된 배열에서 특정 값을 효율적으로 찾기 위한 알고리즘이다.
이 알고리즘은 탐색 범위를 절반으로 줄여 나가면서 목표 값을 찾기 때문에 매우 빠르고 효율적으로 값을 찾을 수 있다.
이 글에서는 이진 탐색의 개념과 구현 방법, 그리고 시간 복잡도를 다뤄보려고 한다.
이진 탐색이란?
이진 탐색은 정렬된 배열에서 원하는 값을 찾기 위해 사용되는 알고리즘이다.
탐색 범위를 절반으로 줄여나가며 목표 값을 찾기 때문에, 탐색 속도가 매우 빠르다.
하지만 이진 탐색을 사용하려면 배열이 정렬되어 있어야 한다는 점이 중요하다.
이진 탐색 동작 과정
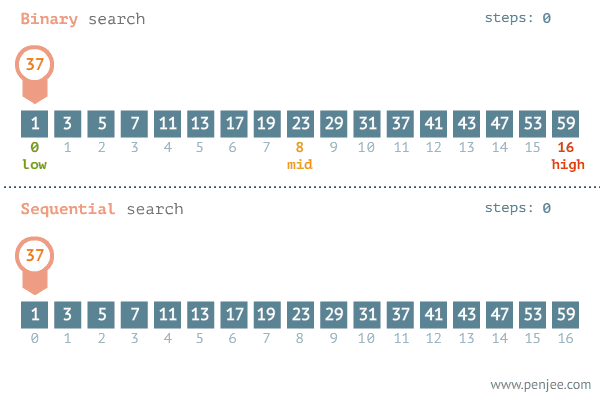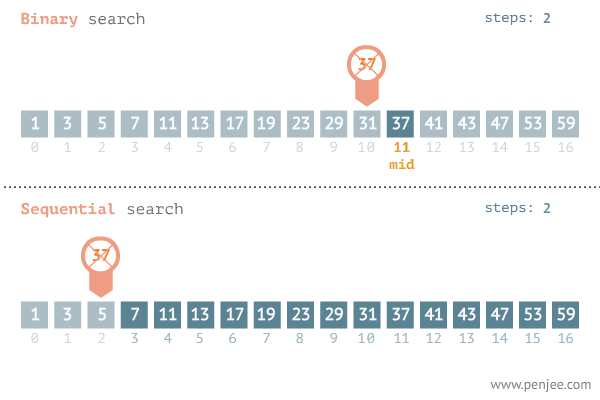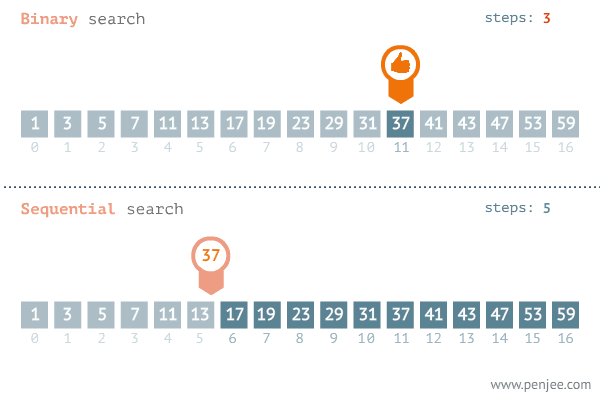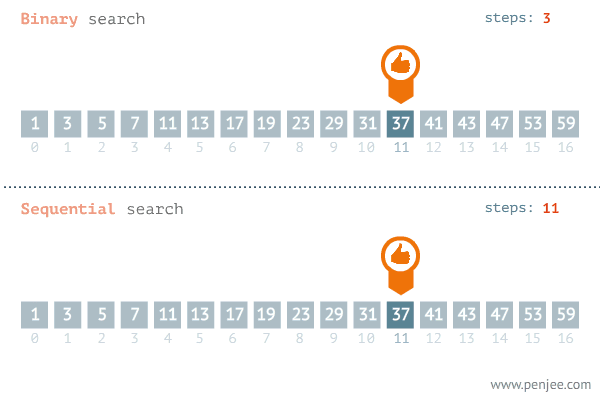
이진 탐색은 다음과 같은 단계로 진행된다:
- 중간값 계산:
- 배열의 중간값을 계산하여 현재 탐색 범위의 중간 인덱스를 구한다.
- 목표 값 비교:
- 중간값이 목표 값과 같으면, 중간 인덱스를 반환한다.
- 중간값이 목표 값보다 작으면, 탐색 범위를 오른쪽 절반으로 줄인다.
- 중간값이 목표 값보다 크면, 탐색 범위를 왼쪽 절반으로 줄인다.
- 반복:
- 위의 과정을 탐색 범위가 소진될 때까지 반복한다. 목푯 값을 찾지 못한 경우 -1 또는 적절한 값을 반환한다.
이진 탐색 예시 :
배열 {1, 3, 5, 11, 13, 17, 20, 31, 32, 35, 59, 72, 86, 90}
목표 값: 11
1. 초기설정
- 배열의 시작 인덱스를 low로 설정한다. 따라서 low = 0이 된다.
- 배열의 끝 인덱스를 high로 설정한다. 배열의 길이가 14라면 끝 인덱스는 13이 된다. 따라서 high = 13이 됩니다.
2. 첫 번째 반복

- mid의 값을 계산한다. mid는 low와 high의 중간 값이다.
- $mid = (low + high) / 2$
- 이를 계산하면, $mid = (0 + 13) / 2 = 6.5$
- mid는 정수형으로 취급되므로, 소수점 이하를 버리고 6이 된다.
- 이제 numbers[mid]와 목표 값을 비교한다.
- 만약 numbers[mid]가 목표 값과 같다면, 목표 값을 찾은 것이므로 mid를 반환한다.
- numbers[mid] = 20 이고, 목표 값 11보다 크므로 탐색 범위를 왼쪽으로 좁혀야 한다.
- 따라서 high 값을 mid - 1로 설정한다. 즉, high = 6 - 1 = 5가 된다.
3. 두 번째 반복

- low = 0
- high = 5
- mid의 값을 다시 계산한다.
- $mid = (low + high) / 2 = (0 + 5) / 2 = 2.5$
- mid는 정수형으로 취급되므로, 2가 된다.
- 이제 numbers[mid]와 목표 값을 비교한다.
- numbers[mid] = 5 이고, 목표 값 11보다 작으므로 탐색 범위를 오른쪽으로 좁혀야 한다.
- 따라서 low 값을 mid + 1로 설정한다 즉, low = 2 + 1 = 3가 됩니다.
4. 세 번째 반복

- low = 3
- high = 5
- mid의 값을 다시 계산한다.
- $mid = (low + high) / 2 = (3 + 5) / 2 = 4$
- 이제 numbers[mid]와 목표 값을 비교한다.
- numbers[mid] = 13 이고, 목표 값 11보다 크므로 탐색 범위를 왼쪽으로 좁혀야 한다.
- 따라서 high 값을 mid - 1로 설정합니다. 즉, high = 4 - 1 = 3가 됩니다.
5. 네 번째 반복

- low = 3
- high = 3
- mid의 값을 다시 계산합니다.
- mid = $(low + high) / 2 = (3 + 3) / 2 = 3$
- 이제 numbers[mid]와 목표 값을 비교한다.
- numbers[mid] = 11 이고, 목표 값 11과 같으므로 목표 값을 찾았다.
- 따라서, 목표 값 11은 배열의 인덱스 3에 위치해 있다는것을 알 수 있다.
이진 탐색의 시간복잡도
이진 탐색의 시간 복잡도는 $O(log n)$이다. 이는 탐색 범위를 매번 절반으로 줄여나가기 때문에 매우 효율적이다. 예를 들어, 배열의 크기가 1,000,000일 때 최대 20번만 비교하면 목표 값을 찾을 수 있다.
예를 들어 배열의 크기를 $n$ 으로 정의하고 $n = 1,000,000$ 일 때 :
- 초기 배열 크기: 1,000,000
- 첫 번째 탐색: 배열을 반으로 줄이면 500,000
- 두 번째 탐색: 다시 반으로 줄이면 250,000
- 세 번째 탐색: 다시 반으로 줄이면 125,000
- 네 번째 탐색: 다시 반으로 줄이면 62,500
- 다섯 번째 탐색: 다시 반으로 줄이면 31,250
- 여섯 번째 탐색: 다시 반으로 줄이면 15,625
- 일곱 번째 탐색: 다시 반으로 줄이면 7,812
- 여덟 번째 탐색: 다시 반으로 줄이면 3,906
- 아홉 번째 탐색: 다시 반으로 줄이면 1,953
- 열 번째 탐색: 다시 반으로 줄이면 976
- 열한 번째 탐색: 다시 반으로 줄이면 488
- 열두 번째 탐색: 다시 반으로 줄이면 244
- 열세 번째 탐색: 다시 반으로 줄이면 122
- 열네 번째 탐색: 다시 반으로 줄이면 61
- 열다섯 번째 탐색: 다시 반으로 줄이면 30
- 열여섯 번째 탐색: 다시 반으로 줄이면 15
- 열일곱 번째 탐색: 다시 반으로 줄이면 7
- 열여덟 번째 탐색: 다시 반으로 줄이면 3
- 열아홉 번째 탐색: 다시 반으로 줄이면 1
배열의 크기가 1,000,000일 때 이진 탐색을 통해 최대 20번 이하의 비교로 목표 값을 찾을 수 있다.
따라서 아래와 같은 수식이 성립된다.
$$log_2(1000000) ≈20$$
시간 복잡도에서 흔히 사용하는 $logn$은 기본적으로 로그의 밑이 2인 이진 로그를 의미한다.
이진 탐색의 경우, 탐색 범위를 절반으로 줄이기 때문에 로그의 밑이 2인 경우가 많다.
이진 탐색 구현
1) 반복문을 이용하여 구현
public static int binarySearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (arr[mid] == target) {
return mid;
}
if (arr[mid] < target) {
low = mid + 1;
}
if (arr[mid] > target) {
high = mid - 1;
}
}
return -1;
}
2) 재귀 함수를 이용한 구현
public static int binarySearch(int[] arr, int target, int start, int finish) {
if (finish < start) {
return -1;
}
int mid = start + (finish - start) / 2;
if (arr[mid] == target) {
return mid;
}
if (target < arr[mid]) {
return binarySearch(arr, target, start, mid - 1);
}
else {
return binarySearch(arr, target, mid + 1, finish);
}
}결론
이진 탐색은 정렬된 배열에서 특정 값을 찾는 데 매우 효율적인 알고리즘이다.
탐색 범위를 매번 절반으로 줄여 나가며 목표 값을 찾기 때문에, 대규모 데이터셋에서도 빠른 속도로 원하는 값을 찾을 수 있다 이진 탐색의 시간 복잡도는 $O(log n)$ 으로, 배열의 크기가 커질수록 그 효율성의 장점이 더욱 두드러진다.
이진 탐색의 주요 단점은 데이터가 반드시 정렬되어 있어야 한다는 점이다. 데이터가 정렬되어 있지 않은 경우, 이진 탐색을 사용하기 전에 정렬 과정이 필요하다. 또한, 재귀를 사용하는 구현에서는 스택 오버플로우 문제를 고려해야한다.이진 탐색 알고리즘을 적절하게 활용하면, 효율적으로 데이터를 검색할 수 있으며, 다양한 문제 해결에 큰 도움이 될거같다.
관련 문제
'PS > 탐색' 카테고리의 다른 글
| [알고리즘 | 탐색] 이진 탐색 활용 Lower Bound & Upper Bound 정리 (0) | 2024.08.09 |
|---|---|
| [알고리즘 | 정렬] 선택 정렬 (Selection Sort) 정리 (0) | 2024.08.08 |
| [알고리즘 | 정렬] 카운팅 정렬 (Counting Sort) 정리 (0) | 2024.08.07 |
